モナドって結局何なのよ?¶
Haskell を勉強しようとすると必ず「モナド」ってのが出てきます。困ったものです。数学とか圏論とか関係があるらしくって、何が書いてあるんだか分からなくって嫌になってしまいます。でもね、Haskell って凄いらしいじゃないですか、格好良いらしいじゃないですか。ここはちょっとがんばって色々考えてみましょう。
そもそも Haskell って何なのよ?¶
何なんでしょうね、Haskell って。コンピュータ言語らしいんです、あ、それは分かってると。良く挙げられる性質は次な感じ?:
- 関数型言語
- 強い型付け
- 遅延評価
- 参照透過
ここでちょっと型に関して見てみましょう。試しに Haskell の実装の 1 つである Hugs で 1 について考えてみます。Hugs では :type や :info というコマンドで hugs に型の情報などを質問することができます。例えば、Haskell にとって 1 って何でしょう?:
$ hugs
__ __ __ __ ____ ___ _________________________________________
|| || || || || || ||__ Hugs 98: Based on the Haskell 98 standard
||___|| ||__|| ||__|| __|| Copyright (c) 1994-2005
||---|| ___|| World Wide Web: http://haskell.org/hugs
|| || Bugs: http://hackage.haskell.org/trac/hugs
|| || Version: September 2006 _________________________________________
Haskell 98 mode: Restart with command line option -98 to enable extensions
Type :? for help
Hugs> :type 1
1 :: Num a => a
もぉいきなり分かりません。何でしょう Num ってのは。分からないことはどんどん聞いていきましょう:
Hugs> :info Num
-- type class
infixl 6 +
infixl 6 -
infixl 7 *
class (Eq a, Show a) => Num a where
(+) :: a -> a -> a
(-) :: a -> a -> a
(*) :: a -> a -> a
negate :: a -> a
abs :: a -> a
signum :: a -> a
fromInteger :: Integer -> a
fromInt :: Int -> a
-- instances:
instance Num Int
instance Num Integer
instance Num Float
instance Num Double
instance Integral a => Num (Ratio a)
なるほど、Num というのは type class だそうです。type class?
type class って何なのよ? [1]¶
type class ってのは何だろうと思うわけですが、:info の結果の下に書いてあることで類推してみます。Num ってのは Eq と Show (多分こいつらも type class なんでしょう) の性質を満たしていて、更に (+), (-), (*) という 3 つの二項演算子と negate, abs, signum, fromInteger, fromInt という 5 つの関数が定義されている「何か」なのですね。多分こんなイメージ:
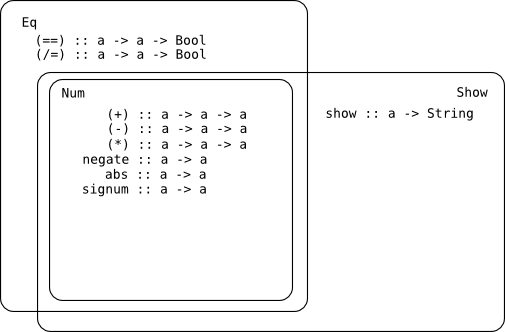
:info Num のイメージ
Num っつーからには数字を抽象化した「何か」に違いなく、例えば:
x + (negate x) = 0 -- プラスマイナス足したら 0
abs (nagete x) = abs x -- マイナス付けても絶対値は変わらない
みたいなのを満たしてるに違いありません。確かに Num の Instance である Int にしろ Float にしろ 0 を持ってたりマイナスや絶対値の計算ができるわけですから、Num はそいつらの持つ共通の性質を抜き出したものに見えます。
何でこんなもん用意しているかというと、同じ性質を持つ人達にまとめてレッテル貼ってひとからげに扱ってあげましょう、ということみたいです。例えば OCaml という、やはり強く型付けられているコンピュータ言語があります。OCaml ももちろん int や float という数値が入る型を持つのですが:
$ ocaml
Objective Caml version 3.11.2
# 1;;
- : int = 1
# 1.0;;
- : float = 1.
# 1 + 1;;
- : int = 2
# 1 + 1.0;;
Error: This expression has type float but an expression was expected of type
int
# 1.0 + 1.0;;
Error: This expression has type float but an expression was expected of type
int
1 は int として、1.0 は float として解釈されてます。int を足すには (+) を使いますが、int と folat は足せません。いわんや int と float をや。じゃぁ float と float なら足せるの? というとやっぱりそれもダメなのです。(+) は int と int を足す為のものなのです。じゃぁどうするのか?:
# 1.0 +. 1.0;;
- : float = 2.
その為には (+.) という別の演算子が用意されているのです。ΩΩ Ω。びっくりしましたか? 私は最初に聞いたときはびっくりしましたがもぉ慣れました。慣れというのは時には偉大なものです。そして OCaml は素敵なものです。
OCaml は強い型付けをしていて、int と float の為に (+) と (+.) という別々の関数を用意しました (float 用はまだまだあります、(-.) とか (*.) とか (/.) とか)。その頃 Haskell はどうしたかというと:
Hugs> :type 1
1 :: Num a => a
Hugs> :type 1.0
1.0 :: Fractional a => a
Hugs> :type 1 + 1
1 + 1 :: Num a => a
Hugs> :type 1.0 + 1
1.0 + 1 :: Fractional a => a
Hugs> :type 1.0 + 1.0
1.0 + 1.0 :: Fractional a => a
え、Fractional?:
Hugs> :info Fractional
-- type class
infixl 7 /
class Num a => Fractional a where
(/) :: a -> a -> a
recip :: a -> a
fromRational :: Rational -> a
fromDouble :: Double -> a
-- instances:
instance Fractional Float
instance Fractional Double
instance Integral a => Fractional (Ratio a)
ほうほう。Fractional という type class があるんだけどそれは Num が元になっていて、更に (/) と recip と fromRational と fromDouble が加わってるものだと。Float や Dobule は Fractional の instance であると。
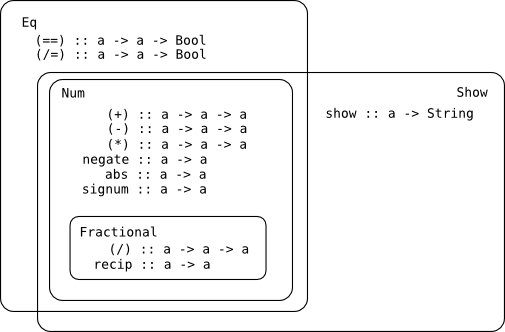
:info Fractional のイメージ
えー、じゃぁ型はどこに行っちゃったの? というと:
Hugs> 1 :: Int
1
Hugs> 1 :: Float
1.0
Hugs> 1.0 :: Int
ERROR - Cannot infer instance
*** Instance : Fractional Int
*** Expression : 1.0
Hugs> 1.0 :: Float
1.0
Hugs> (1 :: Int) + (1 :: Int)
2
Hugs> (1 :: Int) + (1 :: Float)
ERROR - Type error in application
*** Expression : 1 + 1
*** Term : 1
*** Type : Int
*** Does not match : Float
Hugs> (1 :: Float) + (1 :: Float)
2.0
Hugs> :type (+)
(+) :: Num a => a -> a -> a
ほほぉ、1 は Num として解釈されていましたが、Num の instance である Int や Float として型が確定できると。1.0 は Fractional として解釈されるから Int には戻れないけど Float にならなれると。でも Fractional は元に Num があるから (+) とか (-) が使えてしまうのですね。そして、さっき見たように 1 + 1.0 なら Fractional に合わせてくれる。型の確定まで遅延されている! 何かまどろっこしいけどカッコイイよ type class!!
Haskell は type class というのを用意することによって、強い型付けを持ちつつも同じ演算子・関数を複数の似たような型に対して使えるようにしてくれました。
- 有理数は体だけどその前に環であり群だし、加法の記号は一々切り替えたくないよね!
- Interface を用意しといて implement! polymorphism!!
- 似たような機能は一箇所に集めておくのが DRY (Don’t repeat yourself) だよね! (や、それはまた別)
- 仕事のメールには「仕事」ってタグが付いてるけどその中から支払い関連を検索して更に「支払い」ってタグ付けよう!
何でもいいですが、異なる対象に対して同じ名前でアクセスできるのはとても便利そうです。
数字のことはいいから Monad はどうなったのよ¶
はい、Monad のことを忘れてました。Haskell で Monad といったら Maybe Monad です。大抵の入門では Monad として最初に Maybe が出てきます。たまに List が最初のときがあって、酷いやつだと最初に IO が出てきます。Maybe のこと知りたかったら聞きますよね:
Hugs> :info Maybe
-- type constructor
data Maybe a
-- constructors:
Nothing :: Maybe a
Just :: a -> Maybe a
-- instances:
instance Functor Maybe
instance Monad Maybe
instance Eq a => Eq (Maybe a)
instance Ord a => Ord (Maybe a)
instance Read a => Read (Maybe a)
instance Show a => Show (Maybe a)
ありました、Monad。Maybe は Monad の instance らしい。ということは Haskell に聞けばいいはずで、聞いてみると:
Hugs> :info Monad
-- constructor class
infixl 1 >>=
infixl 1 >>
class Monad a where
return :: b -> a b
(>>=) :: a b -> (b -> a c) -> a c
(>>) :: a b -> a c -> a c
fail :: String -> a b
-- instances:
instance Monad Maybe
instance Monad []
instance Monad IO
あら、意外とシンプル。Monad というのは 2 つの演算子 (>>=), (>>)、それと 2 つの関数 return, fail が定義されているだけのものだそうです。Num と比べると随分少ない。Num は 3 個と 5 個でした。この 4 つのことが分かれば Monad が分かる!! と信じてちょっと調べてみましょう。
と思ったんだけど、色々とずるをしましょう。先ず fail:
fail :: String -> a b
fail は使うな っておじいちゃんが言ってましたし、ただエラー吐くだけの為のものみたいなので無視しちゃいましょう、無視無視。
(>>) なんですが、これは (>>=) を使って書けます:
x >> y = x >>= \_ -> y
x を評価してその結果は使わずに y を評価してね、って意味なんですが今は意味は置いといて、単なる略記法なんだということだけ認めて次に進んでしまいましょう。
残るは (>>=) と return です。
Monad って何なのよ?¶
Monad とは何か、というのは (>>=) と return が分かれば良さそうな気がしてきました。で、ここで Monad とは何かを簡単にまとめたものを発表してみましょう。
Monad とは、
- 中にモノが入れられる箱で
- (一般には) 一度中にモノを入れたら取り出せないけど
- 箱の中の箱の中のモノは箱の中には取り出せる
もの。
何だこれは、さっぱり分からない。でもまぁ、これを念頭に見ていくので一度くらい音読しておきましょう。「もなどとはぁ〜」
return は箱に入れること¶
return :: Monad a => b -> a b は、引数を Monad の中につっこみます。こんなイメージ
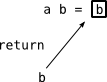
return のイメージ
箱っつーことで a かましたら四角で囲ってみることにしました。で、実際 hugs だとどうなるかというと:
Hugs> return 1
ERROR - Unresolved overloading
*** Type : Monad a => a Integer
*** Expression : return 1
おぉっと、怒られてしまいました。return だけやったら文脈分からんやないけ、ということでしょうか:
Hugs> return 1 :: Maybe Int
Just 1
Hugs> return 1 :: [Int]
[1]
ほっ。return だけだと文脈が分からないので型を指定してやらないといけないのが切ないですが。入れようと思えばいくらでも入れられます。:
Hugs> return (return (return 1)) :: Maybe (Maybe (Maybe Int))
Just (Just (Just 1))
Hugs> return (return (return 1)) :: [[[Int]]]
[[[1]]]
イメージでいうとこんな感じね
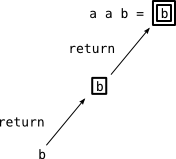
return を 2 回
二回すると二回囲うのね。
どちらも、Int のメンバーを Maybe Int や [Int] といった新天地に導いてくれています。新天地なのでもちろん知らない人達もいるわけです。例えば:
Hugs> :type Nothing
Nothing :: Maybe a
Hugs> :type []
[] :: [a]
Hugs> :type [1,2,3]
[1,2,3] :: Num a => [a]
なんて人達は新天地にしか住んでいない人達で、Int と return からだけでは作れません。とある型を Monad である何かに入れることによって機能拡張してあげようというわけですね。そして古い世界から新天地へと引き上げてくれるのが return です。イメージで上に向かってるのも新天地だからポジティヴな気分で!!
あ、ちなみに、Maybe なら return = Just、List なら return = (:[]) ですねっ!
箱に入れたら liftM でアクセス!!¶
新天地には降りたってみたものの、そのままでは困ったことが起きてしまいます:
Hugs> (1+) 1
2
Hugs> (1+) (Just 1)
ERROR - Cannot infer instance
*** Instance : Num (Maybe a)
*** Expression : 1 + Just 1
Hugs> ((Just 1)+) (Just 1)
ERROR - Cannot infer instance
*** Instance : Num (Maybe a)
*** Expression : Just 1 + Just 1
Int のままだったら (+) で足し算できたのに、Maybe に入れてしまったが為に足し算できなくなってしまいました。恐るべし型付け。このままでは Maybe Int 用にまた一から関数を定義しなくてはいけないのか!? そうではなくて、既存の Int 関連の関数を Maybe など Monad という箱の中に入れる関数が用意されています。:
Hugs> :load Monad
Monad> :type liftM
liftM :: Monad a => (b -> c) -> a b -> a c
lift! M は Monad の M ですね、きっと。liftM は b -> c という関数を a b -> a c という関数に変換してくれてます。a は Monad、つまり新天地なので、b -> c を新天地へと導いて活躍させてあげようというわけです。ありがたやありがたや。
これまたイメージを描いておくと

liftM のイメージ
lift ってことで f が新天地へと持ち上げられてますね。liftM の結果も四角で囲うことにしちゃいました。
で、具体的にどう使うのよ、というと:
Monad> liftM (1+) (Just 1)
Just 2
Monad> liftM (1+) [0..9]
[1,2,3,4,5,6,7,8,9,10]
Monad> liftM return [0..9] :: [[Int]]
[[0],[1],[2],[3],[4],[5],[6],[7],[8],[9]]
新天地のそのまた新天地なんていう遥か彼方へとあの人が旅立ってしまったとしても:
Monad> liftM (liftM (1+)) (Just (Just 1))
Just (Just 2)
liftM を繰り返すことによって箱の中の中へと手が届くようになっています。
これで、新天地でも昔と同じようなことができるようになりました。
(>>=) は分かりづらいから join にしよう¶
次に (>>=) を説明しないといけないんですが、止めましょう。(>>=) は説明しづらいです、私にはできません。なので代わりに先ず join を説明します。join って何だ?:
Monad> :type join
join :: Monad a => a (a b) -> a b
join を使って後で (>>=) のこと説明するからちょっと待っててね。
join は箱を剥すこと¶
join の型を見ると、二重になっている Monad が一重になっています。こ、これは、剥がしている! というわけでこんなイメージ
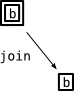
join のイメージ
Maybe や List で見てみると:
Monad> join (Just (Just 2))
Just 2
Monad> join (Just (Just (Just 2)))
Just (Just 2)
Monad> join [[1], [2,3], [4,5,6]]
[1,2,3,4,5,6]
Monad> join [[[1], [2,3]], [[4,5,6], [7,8,9,10]]]
[[1],[2,3],[4,5,6],[7,8,9,10]]
うん、剥がしてる。もっというと、外側から二枚掴んで内側の箱を剥がしてる、それが Maybe だと分かりづらいですが List の場合には見てとれると思います。Maybe の場合は 2 つ続いている Just を 1 つにしているし、List の場合は外側から二枚目のリストを外して平にしたリストを返しています。これは concat のことですね:
Monad> :t concat
concat :: [[a]] -> [a]
残念なことに? join の定義を見ると引数は、a (a b) となっているので、二重の箱に入っていなくてはいけません。箱が一重のときに join を適用しようとしても怒られてしまいます:
Monad> join (Just 3)
ERROR - Cannot infer instance
*** Instance : Num (Maybe a)
*** Expression : join (Just 3)
Monad> join [3]
ERROR - Cannot infer instance
*** Instance : Num [a]
*** Expression : join [3]
一度覚えた贅沢は忘れられない、ことを表現したいのかもしれません。はたまた黄泉戸喫してしまった伊邪那美命のようなものか。あなどりがたし、join。
というわけで
- (一般には) 一度中にモノを入れたら取り出せないけど
- 箱の中の箱の中のモノは箱の中には取り出せる
わけです。(一般には) って付けてるのは、Just 3 からは 3 はそりゃ取り出せますけど Nothing からは何も出てこないし、[1] からは 1 出せるし head [1,2,3] は 1 かもしれませけど、[1,2,3] から 1,2,3 を取り出すって、意味分かりませんもんね。あと、Haskell 的には副作用は IO の中に閉じ込めておきたいので、IO から何か取り出そうとすると「おいおい」って言われるわけです。
と思ったら、Nothing はいくら join してもいいみたい:
Monad> join Nothing
Nothing
Monad> (join . join) Nothing
Nothing
Monad> (join . join . join . join . join . join) Nothing
Nothing
Monad> :t (join . join . join . join . join . join) Nothing
(join . join . join . join . join . join) Nothing :: Maybe a
まぁ Maybe が入れ子になってたら一番外側の Maybe で Nothing のとき Maybe の深さなんて分からないか、と思ったけど型が Maybe a ってなってる。何で??
ここまでまとめ¶
私達は次の 3 つの関数を手に入れた:
return :: Monad a => b -> a b
liftM :: Monad a => (b -> c) -> a b -> a c
join :: Monad a => a (a b) -> a b
それぞれ
- 箱の中にモノを入れる
- 箱の中のモノに関数を適用する
- 二重になってる箱を一重にする
という機能を持っている。
で、この 3 つのセットのことを Monad と言いたい!! まぁ言いたきゃ言えばいいのかもしれませんが、もう少し良い性質を持つときに Monad と呼んであげることに世間ではなっているようなのでもう少し我慢してみましょう。
return と liftM と join の○○な関係¶
さてさて、Monad ってのは不思議な箱で
- 入れるのに return
- 中身をいじるのに liftM
- 過剰包装を剥ぐのに join
を使うというものでした。これらの操作が沢山繰り返されるわけですが、例えば
「入れて入れて剥いだら、入れた状態に戻ってた方が良ぐね?」
って思ったりしませんか? というわけで Monad を使い易くする為に幾つかのルールが設定されているのでそれを見ていきましょう。
まずは次の 2 つ、Monad a と f :: b -> c に対して:
(liftM f) . return = return . f :: b -> a c
(liftM f) . join = join . (liftM (liftM f)) :: a (a b) -> a c
は、それぞれ
- 「箱の中に入れてから f でいじる」=「f でいじってから箱の中に入れる」
- 「1つ箱を剥がしてから中を f でいじる」=「中の中のを f でいじってから1つ箱を剥がす」
という意味になっています。この辺りの操作は順番に依らずにいて欲しいものですよね。イメージで見るとこんな感じ

return と join と liftM に満たしてほしい関係
2 つの四角の中に 2 つずつ赤い道が示してありますが、どっちの道を通っても結果は同じですよ、ということで、真ん中にある「くるん」としてる矢印でもそれを表してるつもりです。
Maybe や List というのはシンプルな Monad なので確かめるのも簡単です。例えば List の場合を見ると:
((liftM f) . return) x = (liftM f) [x] = [f x] = return (f x) = (return . f) x,
((liftM f) . join) [[x, y], [z, w]] = (liftM f) [x, y, z, w] = [f x, f y, f z, f w],
(join . (liftM (liftM f))) [[x, y], [z, w]] = join [liftM f [x, y], liftM f [z, w]]
= join [ [f x, f y], [f z, f w]] = [f x, f y, f z, f w]
みたいな感じになっています。雰囲気だけですが。
更に、Monad であるからには満たして欲しい関係が 3 つ(3 つも!!) あります。Monad a に対し:
join . return = id :: a b -> a b
join . (liftM return) = id :: a b -> a b
join . join = join . (liftM join) :: a (a (a b)) -> a b
この 3 つはいわゆる Monad 則になってるんですが、上の 2 つは既に箱の中に入ってるものへの操作で
- 更に箱に入れて直ぐに剥いだら元に戻る
- 箱の中のものを箱に入れて、その外側から剥いだら元に戻る
最後の 1 つは三重になっている箱に対して
- 「外側から順番に剥がす」=「内側から順番に剥がす」
と言っています。内の方から剥がせるなんて何て器用な、とも思いますが、まぁそれも liftM の底力。
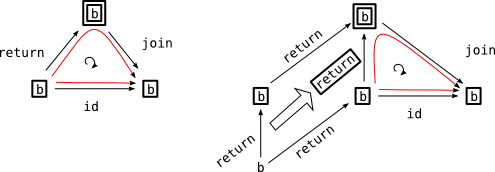
join . return = id と join . (liftM return) = id

join . join = join . (liftM join)
数学嫌と言いながらいつの間にか数学になっちゃってるんですが、最初の 2 つに関しては:
(join . return) [1,2,3] = join [[1,2,3]] = [1,2,3],
(join . (liftM return)) [1,2,3] = join [[1], [2], [3]] = [1,2,3]
みたいなことですね。最後のやつは:
(join . join) [[[1],[2,3]],[[4,5,6],[7,8,9,10]]]
= join [[1],[2,3],[4,5,6],[7,8,9,10]]
= [1,2,3,4,5,6,7,8,9,10]
(join . (liftM join)) [[[1],[2,3]],[[4,5,6],[7,8,9,10]]]
= join [join [[1],[2,3]], join [[4,5,6],[7,8,9,10]]]
= join [[1,2,3], [4,5,6,7,8,9,10]]
= [1,2,3,4,5,6,7,8,9,10]
まぁ、そりゃどっちも同じになりますよね。でも一応手順が違うんだけど結果が同じになってるところだけお楽しみ下さい。
Monad とは¶
Haskell における Monad とは、type class であって Monad a に対して関数:
return :: b -> a b
liftM :: (b -> c) -> a b -> a c
join :: a (a b) -> a b
の 3 つの関数が定義されていているもの。で、コンパイラなどではチェックされないけれども、関数達の関係式:
(liftM f) . return = return . f
(liftM f) . join = join . (liftM (liftM f))
及び:
join . return = id
join . (liftM return) = id
join . join = join . (liftM join)
が仮定されている。
「おい、(>>=) はどこいった!」
join to (>>=)¶
覚えてましたか、(>>=) のこと。残念です。や、流石でいらっしゃる。安心して下さい、(>>=) は join で書けるんです:
x >>= f = (join . (liftM f)) x
これで OK です。
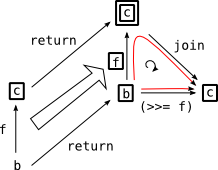
join から >>= のイメージ
何でか:
Monad a
x :: a b
f :: b -> a c
としたときに:
liftM f :: a b -> a (a c)
liftM f x :: a (a c)
join (liftM f x) :: a c
なので、確かに:
(>>=) :: a b -> (b -> a c) -> a c
となっています。では、これどういう操作をしてるか見てみると、
- x の中にいる b を f でいじるのに liftM 使ったら沢山包まれちゃったんで最後に剥がした
ですって。なるほど、(>>=) ってそういうことだったのか!! や、これも解釈の 1 つですが。えっ、何言ってるの? という人は今こそ モナドの全ての例 を見るときがやってきました。いってらっしゃい!!
(>>=) のことをもう少し¶
数学なんて良く分からないなんて言っていましたが、そろそろ数学の話をしましょう。
実は、liftM に関して欲しい性質を隠していました:
liftM id = id
liftM (g . f) = (liftM g) . (liftM f)
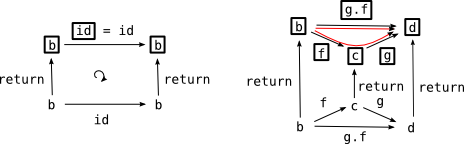
liftM の満たすべき性質
liftM は圏論の関手というやつの射に対する作用を表現するものにそっくりなのです。Data.Functor.fmap そっくりなのです。なのでこの際この性質を仮定してしまいましょう。だってまぁ、
- 何もしない id で中身をいじっても何も変わらない
- まとめて中をいじるのも、少しずつ中をいじるのも同じ
というのが自然だと思いませんか? 私は自然だと思います。
さて、この仮定の下に x >>= f の f を id :: (a (a b)) -> a (a b) としてみると:
x >>= id = join (liftM id x) = join x
(>>= id) = join と、join を再構成することができました。
更に、join の Monad 則からスタートしてごちゃごちゃいじると:
join . return = id
=> join (return (f x)) = f x -- 両辺を f x に作用させた
=> join (liftM f (return x)) = f x -- return と liftM の関係を使った
=> (return x) >>= f = f x -- (>>=) の定義
join . (liftM return) = id
=> (join . (liftM return)) x = x -- 両辺を x に作用させた
=> x >>= return = x -- (>>=) の定義
と前半の 2 つは直ぐに分かります。
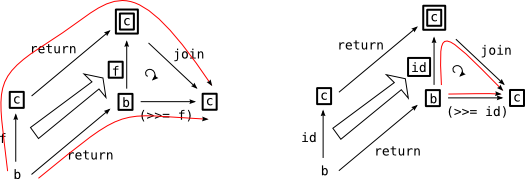
(>>=) と return の関係のイメージ
最後の 1 つに関しても:
join . join . (liftM (liftM g)) . (liftM f) $ x
= join . (liftM g) . join . (liftM f) $ x -- join と liftM の関係
= join . (liftM g) $ x >>= f -- (>>=) の定義
= (x >>= f) >>= g -- (>>=) の定義
join . (liftM join) . (liftM (liftM g)) . (liftM f) $ x
= join (liftM (join . (liftM g) . f) x) -- liftM への仮定の 2 つめ
= x >>= (join . (liftM g) . f) -- (>>=) の定義
= x >>= (\y -> (f y >>= g)) -- lambda で書いて (>>=) の定義
join . join = join . (liftM join)
=> (x >>= f) >>= g = x >>= (\y -> (f y >>= g))
と (>>=) に書き直すことができました。
図で見るならこう:
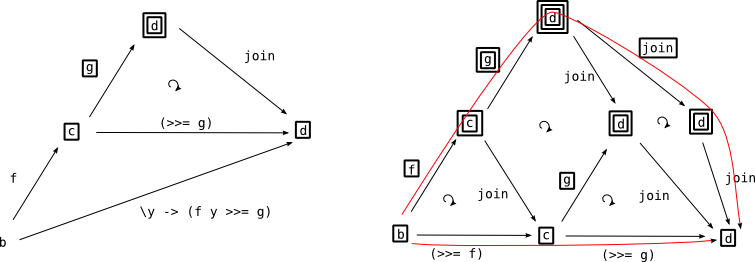
(>>=) の結合律を join のそれから
まとめて:
(return x) >>= f = f x
x >>= return = x
(x >>= f) >>= g = x >>= (\y -> (f y >>= g))
そう、これが (>>=) に関する Monad 則です。join の Monad 則と、return や liftM との関係・仮定を用いて、(>>=) の Monad 則を導くことができました。
そろそろ Haskell の Monad に帰ろうじゃないか¶
join なんて引っぱりだして遠回りしましたが、Haskell の Monad ってのは:
class Monad a where
return :: b -> a b
(>>=) :: a b -> (b -> a c) -> a c
(>>) :: a b -> a c -> a c
fail :: String -> a b
で定義されている type class でした。で、特に return と (>>=) にだけ注目して (>>) と fail は無視することにしてしまいました。:info で見ても出てきませんが、Monad の instance を作るときに作者は次の 3 つの等式が成り立つことを保証しなくてはいけません:
(return x) >>= f = f x
x >>= return = x
(x >>= f) >>= g = x >>= (\y -> (f y >>= g))
これが Monad 則というやつで、コンピュータにこれを保証しろというのは難しいので人間が実装するときに保証するわけです。
で、join や liftM というのはちゃんと Control.Monad で定義されていまして:
join = (>>= id)
liftM f x = x >>= (return . f)
となっています。この定義と (>>=) の Monad 則から:
liftM id = id
liftM (f . g) = (liftM f) . (liftM g)
(liftM f) . return = return . f
(liftM f) . join = join . (liftM (liftM f))
join . return = id
join . (liftM return) = id
join . join = join . (liftM join)
といった等式が再現される、はず。
なので、どちらが偉いとかではなく、分かり易いときに分かり易い方を選べばいいのです。
じゃぁ何で join で説明したのよ、(>>=) のこと嫌いなんでしょ!¶
や、でも、実際 join って使うんでしょうか? Haskell でのプログラミング経験もそんなにないですが、でも join は使ったことがありません。何故でしょう? それはきっと Monad の何が嬉しいかっということに関係してくる、はず。
Monad の何が嬉しいか、そう、それですよね。Monad とか言われて具体例を知って、何だか便利そうなことは分かっても、じゃぁ Monad って何でしょう? と問われると答えられないわけです。でもそれではあんまりだと思ったのでちょっと考えました。で、何が嬉しいかっていうと、関数の返り値の構造を豊かにできるのが嬉しいのだな、と思いました。
型で言うと Monad a => b -> a c のこと。そう、(>>=) の右側に来る奴のことです。
- Maybe だったら普通の値を返すしかないところを Nothing も取る可能性を与え
- List は非決定的な計算とか言ってるけどまぁ、有り得る返り値の集まりを返し
- IO だったら副作用を含むことを示し
- Reader/Writer/State などは計算の返り値とは別に状態を保持し
- Cont は返り値を使って残りの計算がどのようにされるかの設計図を返し
と、b -> a c は、そもそもある計算に加え何かしらの付加情報を与えています。で、その計算を 1 つだけしても仕方無いでしょ? 返り値を使ってまた計算して返り値を使ってまた計算して、そして大きな計算をしたいわけでしょ? というわけで b -> a c を繋げて・合成していきたいわけです。それが正に:
(x >>= f) >>= g = x >>= (\y -> (f y >>= g))
ではないですか。これは「順々に作用させる」のと「合成させたのを作用させる」のが同じだって言ってますもん。正に Monad の嬉しいことに関する性質を一言で表現してくれて、いるとは言い難い、けど、表現してる。スタートの x は return b でも何でもいいんです。その後で、f をして g をして、と、付加情報を使いながら計算を続けていけることが素敵なんです。で、それを表すのには join よりも (>>=) の方がよっぽど素敵なんです。素敵とかいって適当に褒めてはいけません、使い易いしやりたいことずばりそれを表現してくれているのです。
なので、Haskell で Monad を説明したかったらそりゃ (>>=) の使い方を知ろうってことになると思うんですが、私は join が分かって何したいのかが少し分かるようになったので join から話を流してみました。
Monad はこれだけじゃないんだよ¶
Monad の定義を 2 つ見ました
- return, (>>=), Monad 則
- liftM, return, join, liftM 関連の性質, Monad 則
2 つ見ただけで十分疲れちゃいましたけど、まだあるんです。
Kleisli 合成¶
それがこれ:
-- | Left-to-right Kleisli composition of monads.
(>=>) :: Monad m => (a -> m b) -> (b -> m c) -> (a -> m c)
f >=> g = \x -> f x >>= g
ここまで Hugs でがんばってきましたか、ちょびっと GHC からソースを借りてきました。定義を見ると、(>>=) の Monad 則の最後の f と g が出てくるやつ:
(x >>= f) >>= g = x >>= (\y -> (f y >>= g))
の右辺の右側とそっくりそのままですね。a -> m b の形の関数の合成を表してるのが (>=>) です。

三位一体のモナド
さて、これを使うと Monad 則は:
(return x) >>= f = f x
=> (\y -> return y >>= f) x = f x -- lambda で書いてみた
=> return >=> f = f -- (>=>) の定義
x >>= return = x
=> (f x) >>= return = f x -- x を f x に置き換え
=> (\y -> (f y) >>= return) x = f x -- lambda で書いてみた
=> f >=> return = f
(x >>= f) >>= g = x >>= (\y -> (f y >>= g))
=> (h x >>= f) >>= g = (h x) >>= (\y -> (f y >>= g)) -- x を h x に置き換え
=> ((\y -> (h y >>= f)) x) >>= g = (\z -> (h z) >>= (f >=> g)) -- lambda にしてみた
=> ((h >=> f) x) >>= g = h >=> (f >=> g) -- (>=>) の定義
=> (\z -> ((h >=> f) z) >>= g) x = h >=> (f >=> g) -- も一度 lambda にしてみた
=> (h >=> f) >=> g = h >=> (f >=> g) -- (>=>) の定義
つまり、次の 3 つに書き換えられます:
return >=> f = f
f >=> return = f
(f >=> g) >=> h = f >=> (g >=> h)
これが (>=>) の Monad 則になります。これは、何かとってもコンパクトですね。(>=>) を * に、return を E に、f,g,h を A,B,C に書き換えてみると:
E * A = A
A * E = A
(A * B) * C = A * (B * C)
おぉぉ。これは数学のモノイドってやつの性質そっくりです。
- E は左から掛けても相手を変えない (左単位元)
- E は右から掛けても相手を変えない (右単位元)
- 3 つのものの * の計算は、その順序に依らない (結合法則)
でも、f >=> g の場合、f の行き先の型と g の引数の型が対応してなきゃいけなかったりして、ちょっと違います。モノイドと似てるから Monad って言う、かどうかは良く知りません。
で、ここで気をつけなくてはいけないのは、単位元は return であって id ではないということです。や、ほら、id って何もしないから、単位元っぽいじゃないですかぁ〜。っていうかぁ〜、普通の関数の合成に関しては単位元じゃないですかぁ〜。でも違うみたいです、でも、id :: (m a) -> m (a) と思えば id だって (>=>) に入れられるのです。それどころか:
(id >=> f) x
= (\y -> id y >>= f) x
= (id x) >>= f
= x >>= f
というわけで (>=>) から (>>=) が復元できました。あとはもぉ、行ったり来たりするだけです。Monad ってのは関数の返り値の空間を豊かにすることで関数を拡張し、その拡張された関数の合成まで上手く定義したもの、と思うのであれば (>=>) はとっても素敵な演算子に見えてきます。
join = (id >=> id) か、訳分かりませんね、ここまでくると:
(>>= f) = join . (liftM f) = id >=> f
join = (>>= id) = (id >=> id)
f >=> g = \x -> (f x >>= g) = join . (liftM g) . f
これで Monad のこともばっちりだね!!¶
ん〜、どうなんでしょう、そうなんでしょうか。ばっちりって何でしょうか。
Monad なんてのは結局ただの type class なのです。似たような操作が沢山あるから、どれでも記号 1 つで使えるようにしてもらったに過ぎません。Monad のこと分かったから世の中に転がってる色々な Monad instance が使いこなせるというわけではありませんし。
世の中の Monad instance 達を使いこなすことによって Monad が分かったと言うならば、ここでやっと Monad のスタート地点に立ったということかもしれません。 数学は言葉 であって、文法や慣用句憶えても作品を楽しむにはまた違った苦労が必要なわけです。
でもまぁ、 「モナドは単なる自己関手の圏におけるモノイド対象だよ。何か問題でも?」 って言ってもいいですけど「モナド? あぁあの入れたり剥いだり中いじったりするやつね」って言えるのも素敵だなって思うんです。
参考資料¶
- http://stefan-klinger.de/files/monadGuide.pdf
- http://folli.loria.fr/cds/1999/library/pdf/barrwells.pdf
圏論の最初から真面目に書いてあるので、読めれば分かるっていう感じの。って前者は適当に読んだんですが後者はあんま読んでません。ごめんなさい。
- http://snak.tdiary.net/20091020.html
- http://en.wikipedia.org/wiki/Monad_(functional_programming)
- http://en.wikibooks.org/wiki/Haskell/Category_theory
The Monad.Reader の Issue 13 の The Typeclassopedia を日本語に訳して下さってる方がいらっしゃいまして、ありがたいことです。join に関しては Wiki にも書いてあるよ、と書いてあったので貼っておきます。(>=>) のことも書いてあります。
脚注
| [1] | リテラルの解釈と型の変換と勘違いしてました。教えてくれた @eagletmt さん、ありがとう! |